9.1 Substitutions and Transformations

The following discussion applies both to permanent rules and rules from the workspace.

A substitution rule defines an equivalency between two pattern expressions. Note that equivalency also includes types, so it is not possible to transform an expression to another type through application of a substitution rule. To determine if a rule can be applied, one of the patterns is matched against the subject. If the match is positive, the subject can be replaced by the other pattern.

Pattern expressions make use of wildcard symbols. The symbol ? denotes an expression element that can match any subexpression. If the entire pattern matches the subject, the subexpression matched by a wildcard replaces the wildcard in the other pattern to produce a replacement expression.

Syntactically, a substitution rule is simply an identity equation. For example, given the equation sin^2? = 1-cos^2?, the left pattern matches sin x^2 with ?=x. As a result, the right pattern supplies the replacement 1-cos x^2 The same equivalency can also be used to transform .{1-cos ln x^2} by matching the right pattern such that ?=ln x; the replacement is then sin ln x^2.

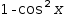
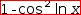
Sometimes more than one wildcard is needed to match a pattern with an expression. In this case the wildcard symbol can be suffixed with a numeric index. For example, one application of De Morgan’s theorem from Boolean Algebra is expressed by the equivalency ¬?1∨¬?2 = ¬(?1∧?2), which can transform ¬A∨¬B into ¬(A∧B) with ?1=A and ?2=B.

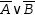
?-wildcards along with their optional numeric suffixes make substitution rules difficult to read. To make patterns more readable, an enhanced notation is provided. In this notation, any single-character lower-case variables map into ?-wildcards with suffixes 1 through 26. Thus the rules above could be written sin^2 x = 1-cos^2 x and ¬a∨¬b = ¬(a∧b) with x, a and b acting as wildcards ?24, ?1 and ?2.

With this definition of pattern variables, it may be useful to reread the first part of this section with the understanding that any single-character lower-case variable denotes a pattern variable. The only exception is function names, which are never used as pattern variables.

Since substitution rules are specified by equations, patterns come in pairs and many of the pairs are reflexive. That is, either pattern of a pair can be tested against a selection and the other pattern provides a candidate for replacement. However, the wildcards on either side of the equation affect reflexivity. A substitution rule is said to be left-to-right if the set of wildcards in the left expression is a superset of the set of wildcards in the right expression. It is said to be right-to-left if the set of wildcards in the right expression is a superset of those in the left expression. When substitution rules are matched, all candidates are the result of testing left to right, right to left, or in both directions as inferred from the rules' wildcard sets.

One substitution rule that is not reflexive is sin^2 ? + cos^2 ? = 1. This is because when 1 matches a literal in an expression, it is not possible to determine what ? should be.

The rule above also shows the use of the same wildcard in two subexpressions. When this is the case, both subexpressions must match. For example, the left side of the rule matches the expression sin (x^2)^2+cos (x^2)^2 with ?=x^2, but does not match sin x^2+cos y^2.

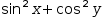
9.1.2 Transformation Patterns

Recall from §3.3.5 that a transform expression consists of type-matched pattern, replacement and constraint expressions. The pattern expression uses wildcard variables described in §3.3.4 and §9.1.1. For transformation patterns, the 27 wildcard variables are augmented by a special wildcard with one of the forms ?(a op ...) or ?(... op z) where op is one of +, -, *. This wildcard matches an expression with a variable number of additive or multiplicative operands. When used in the replacement, wildcards a and z substitute the leading or trailing operand and ... substitutes the rest of the operands. The match will be successful even when the pattern is applied against an unrectified expression.

Another augmented pattern takes the form ?*. This pattern is bound to the entire expression. It is used in the replacement as an argument to some of the transform functions.

9.1.3 Transformation Constraints

Constraints are Boolean expressions that use predicate terms. A predicate term takes the form “wildcard:test” where test is a numeric value, a test selector, or a function. Test selectors are given in Figure 9.1. Figure 9.2 defines predicate functions.

The predicate a:cf(b) succeeds if a matches a product of terms that can be factored by the subexpression matched by b.

The is() function is used to enforce the match of a pattern with a particular operator. Its argument is an expression that contains the operator of interest. For example, the transform 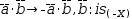ʈa⋅b→-a⋅b, b:is(-X) matches a multiplication operator whose right operand is itself a negation. The argument expression should be kept as simple as possible because only the primary operator is examined. The operands of the argument expression can be any variables that provide a sentential context for the operator. That is, x:is(X*Y) produces the same result as x.is(Y*X). The operands should be variables (i.e., upper-case names) rather than patterns (i.e, lower-case names).

9.1.4 Replacement

The replacement expression contains wildcards supplemented with special functions. The wildcards have values matched from the pattern. The special functions are named after general categories: R for rational and T for transform.

The rational functions perform arithmetic on two-part values representing a fraction. The operands must be known to be constant. That is, a transform with a rational function in the replacement must have a predicate term of the form a:k for each argument to the function.

Transform functions provide access to common transformations.